Software used: MathWorks MATLAB

Publication: A method of determining unified viscoplastic constitutive equations for hot forging simulations, 2016

It is well documented that in the forging process, the material flow patterns, final shape, toolpiece pressure, and overall press load are heavily influenced by the flow stress of a material. In turn, this flow stress is dependent on both strain rate, and temperature. In order to accurately model the forging process, it is necessary for the Finite Element solver to be able to use accurate material properties (i.e. flow stresses) for every element in the workpiece, regardless of its’ temperature and strain rate. In order to achieve this, a set of unified visco-plastic constitutive equations can be used in a subroutine in the solver, which can describe the flow stress of the billet material at a range of temperatures and strain rates. These equations are an analytical representation of a physical material, whose material properties are determined by compressive testing. Through the use of the equations, the FE solver will be able to precisely determine the correct flow stress at a given temperature and strain-rate, regardless of the initial test conditions, and without having to use an inaccurate interpolation.

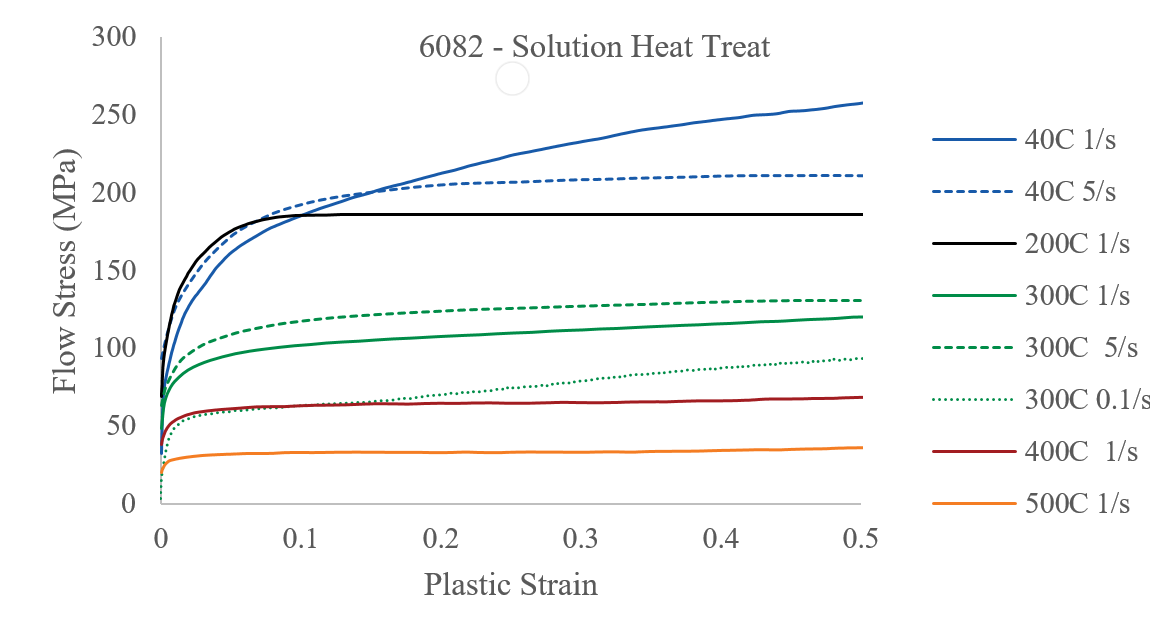
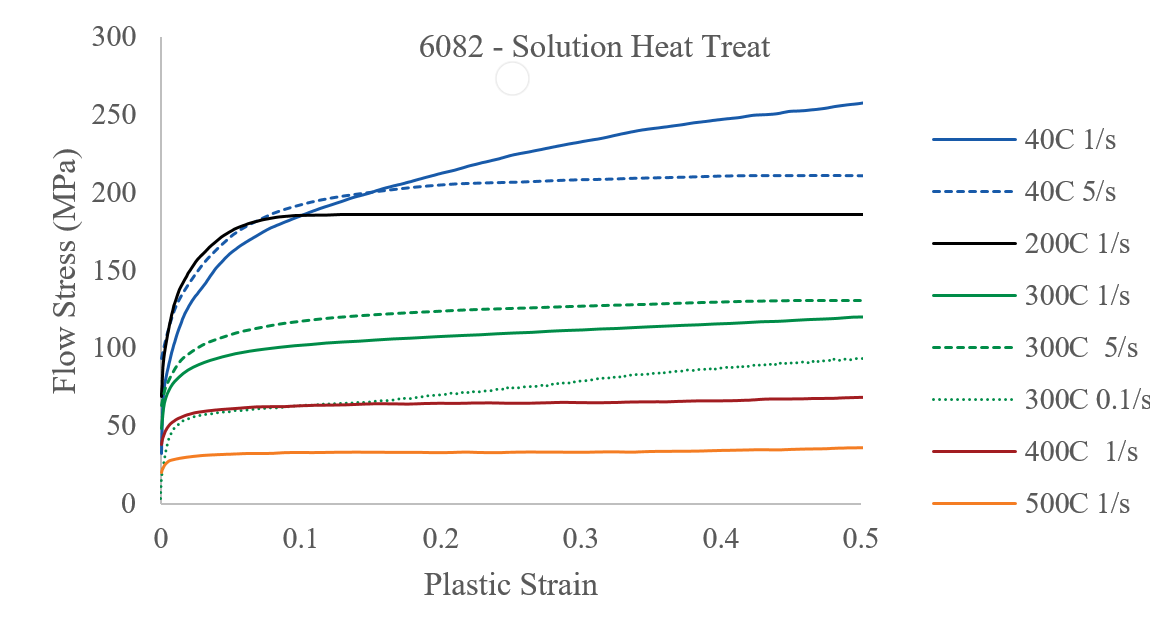
Experimental data was obtained my compressive testing of cylindrical material samples using a Gleeble 3800 thermomechanical testing machine. Steel (EN1A, EN24T), and Aluminium (6082-O, 6082-T4, 7075-T4) alloys were tested at a range of temperatures covering their forming temperatures, and at a range of strain rates (from 0.1 to 10), thus covering a range of forming conditions. Examples of experimental data are shown in the figures.

The constitutive equations used to describe the material properties are standard viscoplastic equations, utilising isotropic hardening and viscoplatic flow terms, as well as Arrhenius temperature dependency. These equations have the notable exception of a damage term, as the forging process is primarily compressive. There are a total of 14 constants to determine, which presents a particularly challenging computational problem.

This project attempts to address the problem by implementing a computational solver which minimises the error between the computational (derived from constants) and experimental material data, utilising readily available, robust optimisation engines.

A series of scripts were written in MATLAB which leverage the built-in Genetic Algorithm solver to quickly determine several “good enough” guesses of sets of constants, then runs the more efficient Simulated Annealing solver to converge upon the best solution. This is a heuristic search method to find a ‘good-enough’ set of constants that minimise error. Given the incredibly large search space, and lack of initial guesses by the user, it is a more realistic approach than attempting to find a single, absolute best set of constants with the lowest possible error.

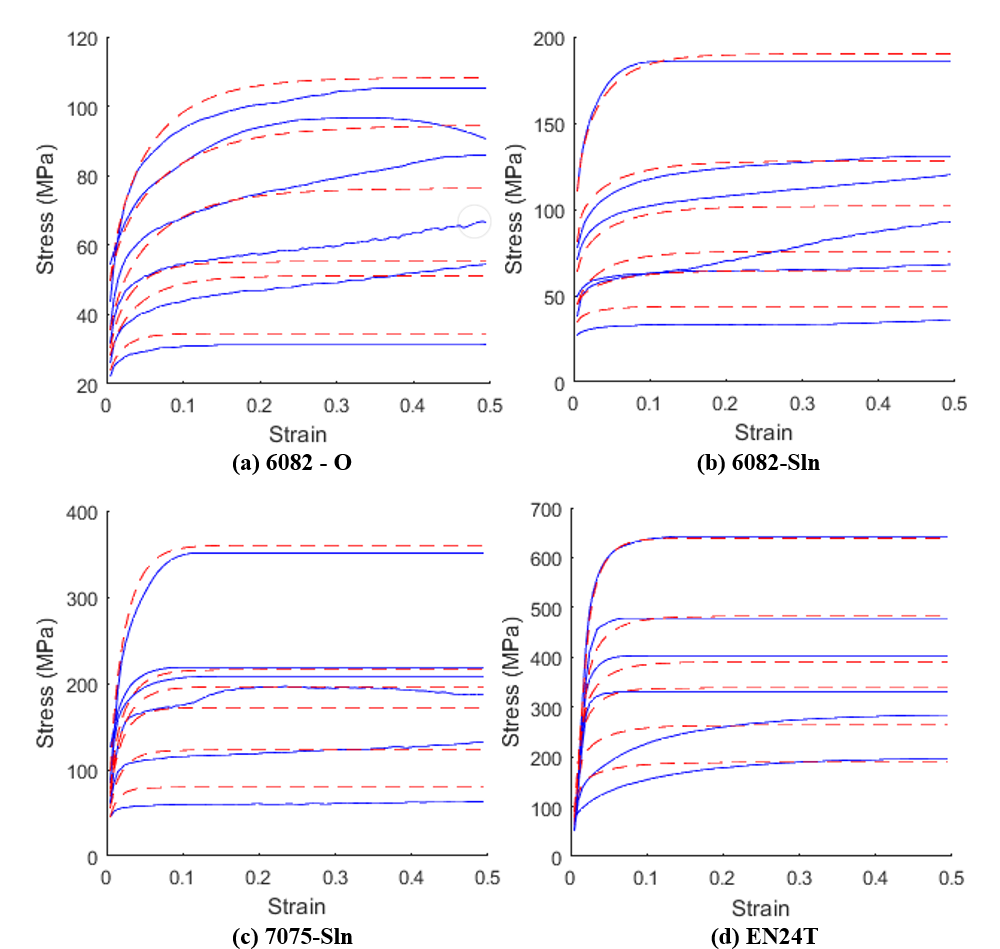
Resulting fits are shown in the images. These fits were obtained within 24 hours on a Core i7-4770, with no initial guesses by the user. The constants can subsequently be used in FE analyses for more accurate material properties.